Сложный процент – что это такое, расчет по формулам с реальными примерами

Содержание

• 1 Что это простыми словами
• 2 Простой и сложный, в чем отличие
• 3 Преимущества и недостатки
• 4 Формулы сложных процентов по вкладам и примеры решения задач
  • 4.1 Формула сложного процента (расчет в годах)
  • 4.2 Формула сложного процента (расчет в месяцах)
• 5 Еще больше примеров
• 6 Примеры сложных процентов в инвестициях
  • 6.1 Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)
  • 6.2 Пример: инвестируем в банк под 8% (срок 20 лет)
  • 6.3 Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)
• 7 Расчет простых процентов

Что это простыми словами

Предлагаем рассмотреть понятие “сложного процента” на примере. Предположим, что вы положили 10 000 рублей в банк на депозитный счет под 10% годовых на 10 лет, без ежемесячных взносов. Через год у вас будет 11 000 рублей. Если прибыль не трогать и оставить на счете, то на следующий год начисления будут производиться от 11 000. Тогда доход составит 1100 рублей, вместо 1000. Спустя 10 лет, следуя этому принципу, у вас будет уже без малого 26 000 рублей.

Год	Базовая сумма начисления	% по депозиту	Итоговая сумма с учетом %
1	10000.00	1000.00	11000.00
2	11000.00	1100.00	12100.00
3	12100.00	1210.00	13310.00
4	13310.00	1331.00	14641.00
5	14641.00	1464.10	16105.10
6	16105.10	1610.51	17715.61
7	17715.61	1771.56	19487.17
8	19487.17	1948.72	21435.89
9	21435.89	2143.59	23579.48
10	23579.48	2357.95	25937.43
Итого		15937.43	25937.43

Простыми словами сложный процент — это когда начисляемые проценты прибавляются к телу вклада и учитываются при дальнейшем начислении прибыли.

Следует отметить, что наибольшую выгоду сложные проценты приносят при долгосрочном инвестировании . Лучше всего это можно заметить, сравнив их с простыми. Поэтому предлагаю разобрать два небольших примера.

1. Представим, вы вложили свои деньги — 100 000 рублей на 10 лет под 15% годовых. Дополнительные взносы отсутствуют, а получаемая прибыль выводится.
2. Во втором случае условия те же, но только прибыль теперь не снимается. А прибавляется к основной сумме вклада и участвует в начислении % каждый год.

Все расчеты приведены в таблице для большей наглядности.

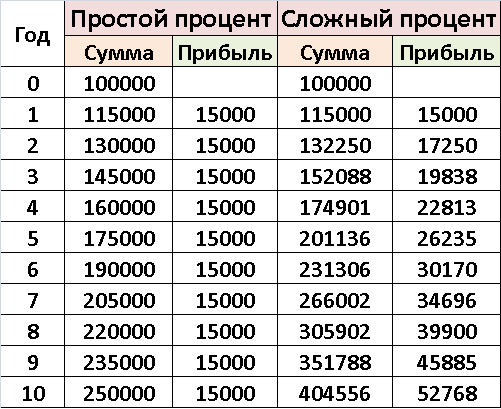
Вы сами прекрасно видите отличие первого варианта от второго. Как одно маленькое условие может кардинально изменить итоговую сумму. Процентная ставка одна и та же, а вот начисления по сложным процентам намного выгоднее, чем по простым. Еще лучше заметна эта разница на графике.

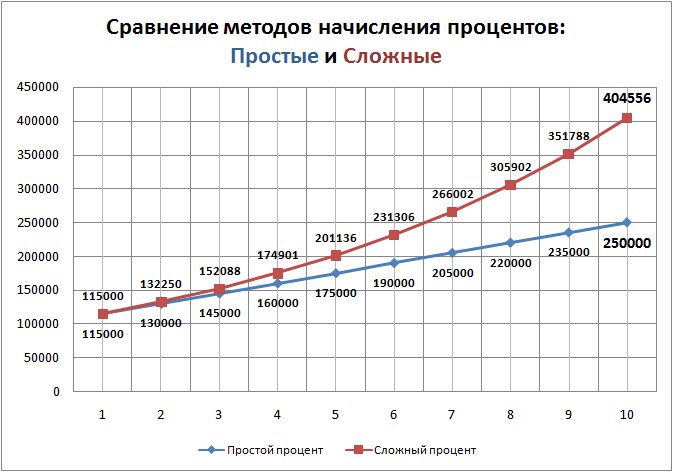
Рост доходности по простым % линейный, а вот по сложным экспоненциальный. Лучше всего это проявляется на длинном промежутке времени. Когда начальный капитал увеличивается в объемах, словно снежный комок. Из периода в период сумма прибыли становится все больше и больше. Способствует этому то, что сама прибыль накапливается и производит новую.

“Сложный процент — это чудо, восьмое чудо света.” Ротшильд

Простой и сложный, в чем отличие

В математике один процент – одна сотая часть числа. Говоря о банковском проценте, обычно подразумевают сумму денег, начисленную по определенным правилам и скопившуюся к конкретному сроку.

Все условия начисления процентов обязательно указываются в договоре между сторонами. Имеют значение такие факторы:

• размер годовой процентной ставки,
• капитализация процентов,
• срок договора,
• порядок выплаты процентов.

Кроме размера ставки, т.е количества начисленных за год процентов, на конечную сумму существенно влияет наличие или отсутствие по условиям договора капитализации процентов.

Капитализация процентов — процесс постоянного добавления начислений к основной сумме.

Это приводит к тому, что один и тот же процент, начисленный в первый период, всегда меньше, чем в последующий – ведь база для исчисления процента вырастает со временем.Такой процент называется сложным процентом.

Во вкладах и кредитах, где база для начисления процента не меняется со временем, всегда остается равной первоначальной сумме, расчет производится по формуле простых процентов.

Преимущества и недостатки

У вкладов, на которые начисляются проценты с капитализацией, имеются свои достоинства и недостатки. Причём зависят они зачастую от условий, которые предоставляет банковская организация. Основным преимуществом подобного вклада является более высокая доходность при определённых условиях.

Из недостатков можно отметить следующее:

1. Нельзя сразу же воспользоваться денежными средствами, полученными за начисление сложных процентов. В депозитах без капитализации проценты сразу же перечисляются на отдельный счёт и доступны для использования вкладчиком.
2. Меньший размер процентной ставки. Некоторые банковские организации выставляют более низкие ставки по вкладам с капитализацией.
3. Низкий уровень доходности при краткосрочных вложениях. Для получения значительной прибыли необходимо размещать денежные средства на срок от 3 лет.
4. Низкая доходность при небольших вкладах.

Учитывая информацию, представленную в этой статье, можно сделать вывод, что депозиты с капитализацией не всегда выгодны. Открывать такой вклад целесообразно только в том случае, если срок депозита будет не меньше 3 лет. Причём при открытии такого депозита рекомендуется использовать крупные суммы денежных средств. В остальных случаях лучше открывать депозиты по другим программам, предлагаемым в различных банках.

 

Формулы сложных процентов по вкладам и примеры решения задач

Формулы сложных процентов в математике встречаются постоянно, особенно если речь идёт об экономических задачах. Представьте, что вам нужно рассчитать прибыль от банковского вклада за несколько лет. Для этого понадобится такая информация:

• начальная сумма вклада (K нулевая или К0)
• ставка доходности (R) — переводится из процентов в число (10% = 0.1)
• количество периодов реинвестирования, то есть лет (n)

А конечную сумму вклада мы назовем просто K. Её можно рассчитать по формуле:

Конечная сумма при расчёте сложных процентов по вкладу

Пример задачи: Инвестор П. положил на депозит в банке 10000$ под 10% годовых. Какую прибыль он получит через 5 лет?

Для начала, давайте узнаем конечную сумму вклада по формуле:

K = 10000$ * (1 + 0.1)5 = 16105.1$

Прибыль (P) — это разница между конечной и стартовой суммой вклада. Считаем:

P = K — К0 = 16105.1$ — 10000$ = 6105.1$

Можно даже подсчитать прибыль в процентах, для этого нужно найти не разницу, а отношение между конечной и стартовой суммой:

P (%) = K/К0 — 1 = 16105.1$ / 10000$ — 1= 61.05%

Используя формулу сложных процентов, вы всегда можете предсказать результат инвестирования в будущем. Впрочем, бывают ситуации, когда вам нужно узнать не конечную, а стартовую сумму вклада. Её можно найти по той же формуле сложных процентов по вкладам, но надо немного её изменить:

Формула расчёта сложных процентов для поиска стартовой суммы вклада

Пример задачи: Инвестор В. хочет узнать, сколько ему надо вложить рублей под 20% годовых сейчас, чтобы через 3 года стать рублёвым миллионером. 

Используем формулу:

К0 = 1000000₽ / (1 + 0.2)3 =  578703.7₽

Кроме суммы вклада, через формулу можно найти и остальные параметры. Например, зная стартовую и конечную сумму, можно узнать процентную ставку или количество периодов реинвестирования.

Начнем с процентной ставки:

Формула расчёта сложных процентов по вкладу для поиска нужной процентной ставки

Пример задачи: Инвестор Р. хочет выяснить, вклад с какой процентной ставкой ему нужен, чтобы заработать 10000$ за 3 года, изначально вложив 20000$.

Для начала нужно посчитать конечную сумму, так как мы знаем только прибыль:

K = К0 + P = 20000$ + 10000$ = 30000$

А теперь можно использовать формулу:

R = (30000$ / 20000$) ^ 1/3 — 1 = 14.47%

Чтобы получить такую доходность, банковский депозит не подойдёт, а вот консервативный ПАММ-счёт — вполне.

Напоследок давайте выясним, как рассчитать, на какой срок нужно положить деньги, чтобы получить нужную нам прибыль. Без логарифмов не обойтись:

Расчёт сложных процентов по вкладу — поиск нужного количества периодов реинвестирования

Пример задачи: сколько лет нужно держать деньги на депозите в банке под 25% годовых, чтобы 50000 рублей превратить в 100000?

Подставляем в формулу:

n = log1+0.25 100000/50000 = 3.11 лет

Кстати, если речь идёт о банке, то 3.11 лет округляются до 4 — вы обычно не можете снять свои деньги до окончания периода действия вклада. Условия конкретного инвестиционного инструмента всегда стоит учитывать при решении подобных задач.

Кроме рассмотренных нами задач существуют и более сложные. Например, довольно распространённая история — у инвестора есть вклад с возможностью пополнения. Часть каждой зарплаты отправляется туда и надо выяснить, какой же будет результат по итогам.

Пример задачи: Инвестор З. вложил 1000$ и откладывает 50$ каждый месяц. Процентная ставка — 1% в месяц. Какая сумма накопится через 5 лет?

Чтобы узнать результат, нужно создать табличку:

Расчёт результатов инвестирования с доливками, с учётом сложных процентов

В первый месяц сумма инвестиций составила 1000$, на неё начислен 1% — итого 1010$. Во второй месяц работают уже 1010$ и еще 50$, которые инвестор внёс дополнительно. Итого — 1070.10. И так далее…

Формула сложного процента (расчет в годах)

Например, вы решили положить 100000,00 руб. под 11% годовых, чтобы через 10 лет воспользоваться сбережениями, которые значительно выросли в результате капитализации. Для расчета итоговой суммы следует применить методику расчета сложного процента.

Применение сложного процента подразумевает то, что в конце каждого периода (год, квартал, месяц) начисленная прибыль суммируется с вкладом. Полученная сумма является базисом для последующего увеличения прибыли.

Для расчета сложного процента применяем простую формулу:

где

• S – общая сумма («тело» вклада + проценты), причитающаяся к возврату вкладчику по истечении срока действия вклада;
• Р – первоначальная величина вклада;
• n - общее количество операций по капитализации процентов за весь срок привлечения денежных средств (в данном случае оно соответствует количеству лет);
• I – годовая процентная ставка.

Подставив значения в эту формулу, мы видим, что:

через 5 лет сумма будет равняться
руб.,

а через 10 лет она составит
руб.

Если бы мы рассчитывали капитализацию процентов по вкладу за короткий период, то сложный процент было бы удобнее рассчитывать по формуле

где:

• К – количество дней в текущем году,
• J – количество дней в периоде, по итогам которого банком производится капитализация начисленных процентов (остальные обозначения – как и в предыдущей формуле).

Но тем, кому удобнее ежемесячно снимать проценты по вкладу, лучше ознакомиться с понятием «капитализация вклада», подразумевающим начисление простых процентов.

На графике показано как вырастет капитал при капитализации процентов по вкладу, если вложить 100000,00 руб. на 10 лет под 10%, 15% и 20%

Формула сложного процента (расчет в месяцах)

Существует и другой, более выгодный для клиента метод начисления и прибавления процентной ставки – ежемесячный. Для этого применяется следующая формула:

где n также соответствует количеству операций по капитализации, но уже выражается в месяцах. Процентный показатель здесь дополнительно делится на 12 потому что в году 12 месяцев, а у нас появляется необходимость в расчете месячную процентную ставку.

Если бы данная формула использовалась для поквартального начисления вклада, то годовой процент делился бы на 4, а показатель n был бы равен количеству кварталов, а если бы процент начислялся по полугодиям, то процентная ставка делилась бы 2, а обозначение n соответствовало количеству полугодий.

Итак, если бы нами был сделан вклад в сумме 100000,00 руб. с ежемесячной капитализацией процентов, то:

через 5 лет (60 месяцев) сумма вклада выросла бы до 172891,57 руб., что примерно на 10000 руб. больше, чем в случае с ежегодной капитализацией вклада;
руб.

а через 10 лет (120 месяцев) «наращенная» сумма составила бы 298914,96 руб., что уже на целых 15000 руб. превосходит показатель, рассчитанный по формуле сложного процента, предусматривающей расчет в годах.

руб.

Это означает, что доходность при ежемесячном начислении процентов оказывается больше, чем при начислении один раз в год. И если прибыль не снимать, то сложный процент работает на пользу вкладчика.

График, показывающий разницу роста капитала при расчете в годах и при ежемесячной капитализации процентов

Еще больше примеров

Выглядит это так: конечная сумма равна начальной, умноженной на сумму единицы и числа равного процентной ставке деленной на 100, в степени равной периоду на который осуществляется вложение (конечная сумма = начальная сумма * (1 + %)n).

В качестве примера не найти ничего лучшего, чем вклад денег на срочный депозит. В реальности для расчета сложных процентов по вкладам банкиры, применяют совершенную формулу имеющую вид: конечная сумма равна, начальной умноженной на единицу плюс процентная ставка деленая на 100, умножить на количество дней, деленное на количество дней в году, все в степени равной периоду вклада (конечная сумма = начальная сумма * (1 + p*d/y)n.

Другими словами, если вы вложили 1000 рублей под 12% годовых, то через год вы получите 1120 рублей. Если на второй год вы продлите вклад не с 1000 рублей а с 1120, то вместо 120 рублей вы уже получите 134,4 р. Кажется не большая разница, но вот что будет за 50 лет:

• Через З года — 1400
• Через 4 года — 1570
• Через 10 лет — 3100
• Через 20 лет — 9640
• Через З0 лет — 29 960
• Через 40 лет — 93 050
• Через 49 лет — 258 040
• Через 50 лет — 289 000

Однако все познается в сравнении и чтобы в полной мере оценить могучий потенциал того, что называется реинвестированием, необходимо сравнить, какие же результаты дают простые и сложные проценты. Если простые проценты дают линейный прирост прибыли, то реинвестиции – это экспоненциальное увеличение капитала, которое тем сильнее, чем большая сумма под больший процент и на дольший срок была вложена.

Таким образом, чем большего размера изначально вы вкладываете капитал, чем дольше он будет лежать на депозите и чем выше установленная для него ставка рефинансирования, тем быстрее и сильнее будет происходить его увеличение, тем самым еще сильнее ускоряя дальнейший процесс.

При необходимости из указанной выше формулы по расчету сложных процентов по банковским вкладам легко выводятся и формулы для определения других необходимых величин: действующей процентной ставки ((конечная сумма/ начальную сумму)1/n – 1); периода, за который из имеющейся суммы потребуется получить искомую (n = log(1+процентная ставка) (конечная сумма / начальную сумму)).

Все бы было здесь прекрасно, если бы не одно «но» – для того, чтобы сложные проценты действительно раскрыли свой полный потенциал и начали наращивать хорошую прибыль, требуется довольно продолжительный срок либо очень высокая процентная ставка, что в честных проектах встречается крайне редко.

А вот пример того, как можно заработать 1 миллион долларов за 11 лет, при условии первоначального вклада три тыс. долларов по 50% годовых, и ежемесячно нужно докладывать по 300 долларов (3600 в год):

1 год $8 565
2 год $17 362
3 год $30 558
4 год $50 351
5 год $80 042
6 год $124 577
7 год $191 381
8 год $291 586
9 год $441 893
10 год $667 355
11 год $1 001 032

Примеры сложных процентов в инвестициях

Можно смело сказать, что каждый рубль отложенный сегодня принесёт десятки рублей через 10 лет за счёт постоянного реинвестирования прибыли. Подобным образом разбогатели многие миллиардеры (Уоррен Баффет).

Мое богатство — это результат комбинации нескольких факторов жизни в США, хороших генов и аккумулирующего эффекта сложных процентов. Уоррен Баффет

Кривые доходности при сложных и простых процентах

Обратите внимание, что эффект заметен со временем все сильнее и в конце кривая сложных процентов приобретает экспоненциальный характер, в то время как простые проценты растут линейно. Рассмотрим на конкретных примерах этот принцип.

Пример: инвестируем ежемесячно в банк под 8% (срок 10 лет)

Если откладывать ежемесячно по 10 тысяч рублей "под подушку" или просто на банковский счёт, то через 10 лет (120 месяцев) сумма будет 1.2 млн рублей (120 умножаем на 10 тыс).

Если же откладывать эти деньги на банковский вклад под 8% годовых, то сумма по истечению 10 лет будет значительно больше 1 851 738 рублей. Чистый доход от процентов 641 738 рублей (чуть больше 50% за все время). Новички по ошибке могут получить неправильную сумму, если просто прибавить 8% к отложенной сумме, но это неверно. Сложный процент можно посчитать лишь на онлайн калькуляторе или самостоятельно с помощью длительных вычислений.

Расчёты на калькуляторе сложных процентов:

Выписка по балансу:

Примечание

В некоторые периоды можно найти ставку на вкладах гораздо выше 8% и доход был бы в таком случае был заметно больше.

Пример: инвестируем в банк под 8% (срок 20 лет)

Теперь увеличим срок нашего инвестирования с 10 лет до 20 лет. Мы будем также откладывать по 10 тысяч рублей и всю полученную прибыль реинвестировать. Теперь по истечению срока сумма будет 5 938 760 рублей вместо 2 400 000. Чистый доход от процентов 3 528 760. Эта сумма больше всех суммарных вложений в 1.5 раза (150% прибыли за все время)!

Это наглядный пример того, что чем больший период мы рассматриваем, тем заметнее будет действие сложных процентов.

Пример: инвестируем в ценные бумаги под 12% (срок 20 лет)

Последний пример. Откладываем также по 10 тысяч рублей ежемесячно на протяжении 20 лет, но теперь мы инвестируем деньги в акции и небольшую часть в облигации. Как показала реальная история, такой инвестиционный портфель в среднем за год приносит 12% с учетом дивидендов от акций при самой простой стратегии "купи и держи".

Итого, сумма на конец срока: 9 999 681 рублей. Чистый доход 7 589 681 рублей. И это не результат везения, не фантастика, а очень реальные цифры дохода, которые доступны каждому лицу! По факту можно даже получить и больше и даже за более короткий срок, если выйти с рынка на его пике, а докупиться в конце цикла падения, но для подобных "маневров" необходимы основы трейдинга и немного времени на совершение торговых операций.

Мы рассмотрели реальные варианты без каких-либо везений и прочее. Такого результата добьется каждый, кто просто вложит в ценные бумаги и не будет дергаться и пытаться что-то еще сделать. Такая стратегия называется: купи и держи.

Примечание

При инвестировании в зарубежные акции доход был бы еще больше (где-то в два раза), поскольку по статистике рубль обесценивается к доллару примерно на 100% каждые 20 лет.

Также важно откладывать в начале как можно больше. Это сильно повышает будущую доходность.

• Как купить акции — подробная инструкция
• Как зарабатывать деньги на акциях
• Стратегии покупки акций
• Дивидендная стратегия
• Стратегии инвестирования на бирже
• Из чего складывается доходность акций

Теперь, понимая силу сложных процентов, поговорим о том, во что лучше всего вложить деньги, чтобы получать пассивный доход. Какие конкретно варианты инвестирования существуют, каковы их риски и преимущества можно прочитать:

• Ценные бумаги и их виды
• Виды акций и их различия
• Облигации — что это такое простым языком
• Инвестиции в акции — полный мануал
• Инвестиции в облигации — что надо знать
• Еврооблигации — как купить и что это
• Что такое ETF фонды

Смотрите также видео про сложные проценты:

Расчет простых процентов

Простые проценты – это проценты, которые начисляются только на сумму основного долга. В каждом конкретном платежном периоде (как правило, месяц) сумма долга разная. Ведь заемщик постоянно ее уменьшает (в идеале). Несмотря на способ погашения кредита (аннутитетными или дифференцированными платежами), формула простых процентов одинаковая.

Формулу можно представить следующим образом:

Проценты = сумма займа (основной долг) * (Ставка в годовых процентах*количество дней в платежном периоде/количество дней в году).  

Например, сумма займа 100 000 руб. Годовая ставка – 6,5%. Срок займа – 200 дней. В году – 366 дней (возьмем для примера високосный год). 

1 случай: кредит погашается единовременным платежом. Тогда проценты за пользование кредитом составят:

100 000 * (6,5%*200/366) = 3500 руб. составит сумма начисленных процентов.

2 случай: кредит погашается ежемесячно. К примеру, расчет за февраль при прочих равных условиях:

100 000 * (6,5%*29/366) = 515,02  руб.